https://programmers.co.kr/learn/courses/30/lessons/77884
코딩테스트 연습 - 약수의 개수와 덧셈
두 정수 left와 right가 매개변수로 주어집니다. left부터 right까지의 모든 수들 중에서, 약수의 개수가 짝수인 수는 더하고, 약수의 개수가 홀수인 수는 뺀 수를 return 하도록 solution 함수를 완성해주
programmers.co.kr
문제
문제 설명
두 정수 left와 right가 매개변수로 주어집니다. left부터 right까지의 모든 수들 중에서, 약수의 개수가 짝수인 수는 더하고, 약수의 개수가 홀수인 수는 뺀 수를 return 하도록 solution 함수를 완성해주세요.
제한사항
- 1 ≤ left ≤ right ≤ 1,000
입출력 예
| left | right | result |
| 13 | 17 | 43 |
| 24 | 27 | 52 |
입출력 예 설명
입출력 예 #1
- 다음 표는 13부터 17까지의 수들의 약수를 모두 나타낸 것입니다.
| 수 | 약수 | 약수의 개수 |
| 13 | 1, 13 | 2 |
| 14 | 1, 2, 7, 14 | 4 |
| 15 | 1, 3, 5, 15 | 4 |
| 16 | 1, 2, 4, 8, 16 | 5 |
| 17 | 1, 17 | 2 |
- 따라서, 13 + 14 + 15 - 16 + 17 = 43을 return 해야 합니다.
입출력 예 #2
- 다음 표는 24부터 27까지의 수들의 약수를 모두 나타낸 것입니다.
| 수 | 약수 | 약수의 개수 |
| 24 | 1, 2, 3, 4, 6, 8, 12, 24 | 8 |
| 25 | 1, 5, 25 | 3 |
| 26 | 1, 2, 13, 26 | 4 |
| 27 | 1, 3, 9, 27 | 4 |
- 따라서, 24 - 25 + 26 + 27 = 52를 return 해야 합니다.
풀이
풀이 과정
총 세 가지의 풀이 방법을 비교해보았다
첫 번째, 1부터 주어진 수 n까지 모든 수를 검사하여 약수의 개수를 확인하는 방법
먼저 어떤 수 n을 입력받아 n의 약수를 구하기 위한 함수를 만들고, 약수의 개수를 저장할 변수를 선언한다
public int divisor_count(int n) {
int count = 0;
}1부터 n까지 반복하며 n을 i로 나누었을 때 나누어 떨어지는 수, 즉 약수의 개수를 카운트하여 return한다
for(int i = 1; i <= n; i++){
if(n % i == 0) count++;
}
return count;divisor_count 함수를 이용하여 left부터 right까지 약수의 개수를 구해 짝수일 경우 더하고 홀수일 경우 빼서 답을 return한다
public int solution(int left, int right) {
int answer = 0;
for(int i = left; i <= right; i++){
if(divisor_count(i) % 2 == 0){
answer += i;
} else {
answer -= i;
}
}
return answer;
}첫 번째 방법의 경우 가장 직관적이고 쉬운 방법이지만 약수를 구할 n값이 커질 수록 오랜시간이 걸리게 된다
두 번째, 1부터 n의 제곱근까지만 확인하여 약수의 개수 구하기
자연수 n은 n의 두 약수 a와 b의 곱으로 나타낼 수 있다
따라서 약수 a를 구하게 되면 항상 그 짝이되는 약수 b가 존재함을 의미한다
그렇기 때문에 for문을 이용하여 자연수 n의 제곱근까지의 약수만 구하면 그 개수의 두 배 만큼의 약수가 있음을 알 수 있다
하지만 n = a * b 일 때 a == b이면, 즉 n이 제곱수 일 경우에 ( 36 = 6 * 6 ) 한 쌍이 아닌 하나의 중복된 값이기 때문에 이 경우를 따로 검사해 주어야 한다
public int divisor_count(int n) {
int count = 0;
for(int i = 1; i <= Math.sqrt(n); i++){
if(n % i == 0){ // i가 n의 약수일 때
if(i * i == n) count++; // i가 n의 제곱근일 경우 count 1만 증가
else count += 2; // 짝을 이루는 약수가 있으므로 count 2 증가
}
}
return count;
}이후의 과정은 첫 번째 풀이와 동일하며 첫 번째 풀이보다 조금 더 효율적으로 계산이 가능하다
세 번째, 제곱수의 성질 이용하기
두 번째 풀이에서 보았듯이 항상 짝을 이루어 존재하기 때문에 자연수 n의 약수의 개수는 2 * i개가 된다
하지만 n이 제곱수일 경우, 중복된 약수 쌍이 하나 포함되어 있기 때문에 약수의 개수가 (2 * i) - 1개가 된다
이를 이용하면 자연수 n이 제곱수가 아닌 경우 약수의 개수는 짝수, 제곱수인 경우 약수의 개수는 홀수임을 알 수 있다
따라서 left부터 right까지 자연수 n이 제곱수인지 아닌지만 확인하면 매우 효율적으로 답을 구할 수 있다
for(int n = left; n <= right; n++){
if(i % Math.sqrt(n) == 0){ // n이 제곱수일 경우 약수의 개수는 홀수
answer -= n;
} else { // n이 제곱수가 아닐 경우 약수의 개수는 짝수
answer += n;
}
}
최종 코드
첫 번째 풀이, 모든 수 검사
class Solution {
public int solution(int left, int right) {
int answer = 0;
for(int i = left; i <= right; i++){
if(divisor_count(i) % 2 == 0){
answer += i;
} else {
answer -= i;
}
}
return answer;
}
public int divisor_count(int n) {
int count = 0;
for(int i = 1; i <= n; i++){
if(n % i == 0) count++;
}
return count;
}
}두 번째 풀이, 주어진 수의 제곱근까지만 검사
class Solution {
public int solution(int left, int right) {
int answer = 0;
for(int i = left; i <= right; i++){
if(divisor_count(i) % 2 == 0){
answer += i;
} else {
answer -= i;
}
}
return answer;
}
public int divisor_count(int n) {
int count = 0;
for(int i = 1; i <= Math.sqrt(n); i++){
if(n % i == 0){
if(i * i == n) count++;
else count += 2;
}
}
return count;
}
}세 번째 풀이, 제곱수의 성질 이용
class Solution {
public int solution(int left, int right) {
int answer = 0;
for(int n = left; n <= right; n++){
if(n % Math.sqrt(n) == 0){
answer -= n;
} else {
answer += n;
}
}
return answer;
}
}성능 비교
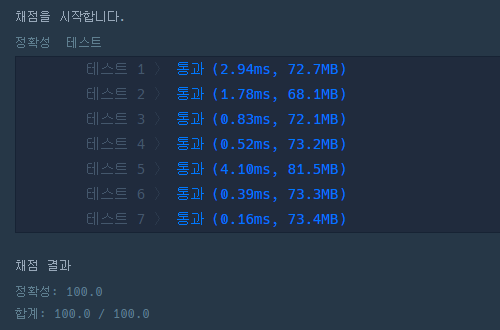

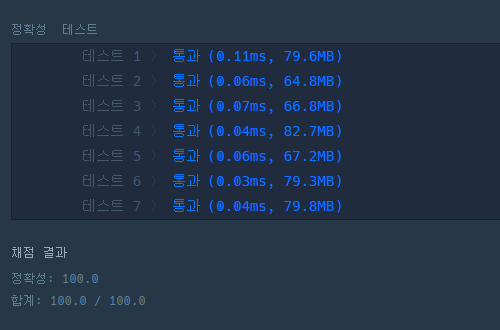
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 타겟 넘버 - Java (4) | 2021.11.10 |
|---|---|
| [프로그래머스] 소수 만들기 - Java (0) | 2021.11.08 |
| [프로그래머스] 폰켓몬 - Java (0) | 2021.11.05 |
| [프로그래머스] 최소직사각형 - Java (0) | 2021.11.04 |
| [프로그래머스] 없는 숫자 더하기 - Java (0) | 2021.11.04 |
https://programmers.co.kr/learn/courses/30/lessons/77884
코딩테스트 연습 - 약수의 개수와 덧셈
두 정수 left와 right가 매개변수로 주어집니다. left부터 right까지의 모든 수들 중에서, 약수의 개수가 짝수인 수는 더하고, 약수의 개수가 홀수인 수는 뺀 수를 return 하도록 solution 함수를 완성해주
programmers.co.kr
문제
문제 설명
두 정수 left와 right가 매개변수로 주어집니다. left부터 right까지의 모든 수들 중에서, 약수의 개수가 짝수인 수는 더하고, 약수의 개수가 홀수인 수는 뺀 수를 return 하도록 solution 함수를 완성해주세요.
제한사항
- 1 ≤ left ≤ right ≤ 1,000
입출력 예
| left | right | result |
| 13 | 17 | 43 |
| 24 | 27 | 52 |
입출력 예 설명
입출력 예 #1
- 다음 표는 13부터 17까지의 수들의 약수를 모두 나타낸 것입니다.
| 수 | 약수 | 약수의 개수 |
| 13 | 1, 13 | 2 |
| 14 | 1, 2, 7, 14 | 4 |
| 15 | 1, 3, 5, 15 | 4 |
| 16 | 1, 2, 4, 8, 16 | 5 |
| 17 | 1, 17 | 2 |
- 따라서, 13 + 14 + 15 - 16 + 17 = 43을 return 해야 합니다.
입출력 예 #2
- 다음 표는 24부터 27까지의 수들의 약수를 모두 나타낸 것입니다.
| 수 | 약수 | 약수의 개수 |
| 24 | 1, 2, 3, 4, 6, 8, 12, 24 | 8 |
| 25 | 1, 5, 25 | 3 |
| 26 | 1, 2, 13, 26 | 4 |
| 27 | 1, 3, 9, 27 | 4 |
- 따라서, 24 - 25 + 26 + 27 = 52를 return 해야 합니다.
풀이
풀이 과정
총 세 가지의 풀이 방법을 비교해보았다
첫 번째, 1부터 주어진 수 n까지 모든 수를 검사하여 약수의 개수를 확인하는 방법
먼저 어떤 수 n을 입력받아 n의 약수를 구하기 위한 함수를 만들고, 약수의 개수를 저장할 변수를 선언한다
public int divisor_count(int n) {
int count = 0;
}1부터 n까지 반복하며 n을 i로 나누었을 때 나누어 떨어지는 수, 즉 약수의 개수를 카운트하여 return한다
for(int i = 1; i <= n; i++){
if(n % i == 0) count++;
}
return count;divisor_count 함수를 이용하여 left부터 right까지 약수의 개수를 구해 짝수일 경우 더하고 홀수일 경우 빼서 답을 return한다
public int solution(int left, int right) {
int answer = 0;
for(int i = left; i <= right; i++){
if(divisor_count(i) % 2 == 0){
answer += i;
} else {
answer -= i;
}
}
return answer;
}첫 번째 방법의 경우 가장 직관적이고 쉬운 방법이지만 약수를 구할 n값이 커질 수록 오랜시간이 걸리게 된다
두 번째, 1부터 n의 제곱근까지만 확인하여 약수의 개수 구하기
자연수 n은 n의 두 약수 a와 b의 곱으로 나타낼 수 있다
따라서 약수 a를 구하게 되면 항상 그 짝이되는 약수 b가 존재함을 의미한다
그렇기 때문에 for문을 이용하여 자연수 n의 제곱근까지의 약수만 구하면 그 개수의 두 배 만큼의 약수가 있음을 알 수 있다
하지만 n = a * b 일 때 a == b이면, 즉 n이 제곱수 일 경우에 ( 36 = 6 * 6 ) 한 쌍이 아닌 하나의 중복된 값이기 때문에 이 경우를 따로 검사해 주어야 한다
public int divisor_count(int n) {
int count = 0;
for(int i = 1; i <= Math.sqrt(n); i++){
if(n % i == 0){ // i가 n의 약수일 때
if(i * i == n) count++; // i가 n의 제곱근일 경우 count 1만 증가
else count += 2; // 짝을 이루는 약수가 있으므로 count 2 증가
}
}
return count;
}이후의 과정은 첫 번째 풀이와 동일하며 첫 번째 풀이보다 조금 더 효율적으로 계산이 가능하다
세 번째, 제곱수의 성질 이용하기
두 번째 풀이에서 보았듯이 항상 짝을 이루어 존재하기 때문에 자연수 n의 약수의 개수는 2 * i개가 된다
하지만 n이 제곱수일 경우, 중복된 약수 쌍이 하나 포함되어 있기 때문에 약수의 개수가 (2 * i) - 1개가 된다
이를 이용하면 자연수 n이 제곱수가 아닌 경우 약수의 개수는 짝수, 제곱수인 경우 약수의 개수는 홀수임을 알 수 있다
따라서 left부터 right까지 자연수 n이 제곱수인지 아닌지만 확인하면 매우 효율적으로 답을 구할 수 있다
for(int n = left; n <= right; n++){
if(i % Math.sqrt(n) == 0){ // n이 제곱수일 경우 약수의 개수는 홀수
answer -= n;
} else { // n이 제곱수가 아닐 경우 약수의 개수는 짝수
answer += n;
}
}
최종 코드
첫 번째 풀이, 모든 수 검사
class Solution {
public int solution(int left, int right) {
int answer = 0;
for(int i = left; i <= right; i++){
if(divisor_count(i) % 2 == 0){
answer += i;
} else {
answer -= i;
}
}
return answer;
}
public int divisor_count(int n) {
int count = 0;
for(int i = 1; i <= n; i++){
if(n % i == 0) count++;
}
return count;
}
}두 번째 풀이, 주어진 수의 제곱근까지만 검사
class Solution {
public int solution(int left, int right) {
int answer = 0;
for(int i = left; i <= right; i++){
if(divisor_count(i) % 2 == 0){
answer += i;
} else {
answer -= i;
}
}
return answer;
}
public int divisor_count(int n) {
int count = 0;
for(int i = 1; i <= Math.sqrt(n); i++){
if(n % i == 0){
if(i * i == n) count++;
else count += 2;
}
}
return count;
}
}세 번째 풀이, 제곱수의 성질 이용
class Solution {
public int solution(int left, int right) {
int answer = 0;
for(int n = left; n <= right; n++){
if(n % Math.sqrt(n) == 0){
answer -= n;
} else {
answer += n;
}
}
return answer;
}
}성능 비교



'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 타겟 넘버 - Java (4) | 2021.11.10 |
|---|---|
| [프로그래머스] 소수 만들기 - Java (0) | 2021.11.08 |
| [프로그래머스] 폰켓몬 - Java (0) | 2021.11.05 |
| [프로그래머스] 최소직사각형 - Java (0) | 2021.11.04 |
| [프로그래머스] 없는 숫자 더하기 - Java (0) | 2021.11.04 |
