https://leetcode.com/problems/minimum-path-sum/description/
Minimum Path Sum - LeetCode
Can you solve this real interview question? Minimum Path Sum - Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path. Note: You can only move either down or rig
leetcode.com
문제
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example 1:
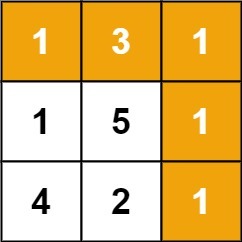
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.
Example 2:
Input: grid = [[1,2,3],[4,5,6]]
Output: 12
Constraints:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 200
- 0 <= grid[i][j] <= 100
풀이
풀이 과정
양수값으로 이루어진 m x n 크기의 그리드가 주어졌을 때 왼쪽 상단지점에서 출발하여 오른쪽 하단에 도착하면서 지나는 지점들의 최소합을 구하는 문제이다.
다른 지점으로 이동하기 위해서는 오른쪽이나 아래쪽으로만 이동이 가능하다. 따라서 (a, b)지점으로 이동할 때의 경로 최소값은 왼쪽 지점 (a, b - 1)의 값과 위쪽 지점 (a - 1, b)의 값 중 최소값과 현재 지점의 값의 합이 된다.
다만 현재 탐색 지점이 가장 위쪽에 있는 경우에는 비교할 위쪽 지점이 없으므로 현재 지점의 값과 왼쪽 지점의 값의 합이 되고, 현재 탐색 지점이 가장 왼쪽에 있는 경우에는 비교할 왼쪽 지점이 없으므로 현재 지점의 값과 위쪽 지점의 값의 합이된다.
시작점(0, 0)부터 한 줄씩 탐색하며 값을 갱신하여 최종적으로 오른쪽 아래 지점의 값을 return 해준다.
1번 예시의 탐색과정을 그림으로 나타내면 다음과 같다.
우선 시작점은 변하지 않는 값이므로 탐색에서 제외한다.

다음으로 오른쪽 지점을 탐색한다. 현재 탐색중인 지점이 가장 위쪽에 있으므로 현재 지점의 값과 왼쪽 지점의 값의 합을 현재 지점의 값으로 저장한다.
현재 행의 나머지 지점에 대해서도 같은 탐색을 통해 값을 저장한다.

한 행에 대한 탐색이 종료되면 다음 행으로 넘어가 탐색을 계속한다.
두 번째 줄의 첫 번째 지점의 경우 가장 왼쪽에 존재하는 지점이므로 현재 지점의 값과 위쪽 지점의 값의 합을 현재 지점의 값으로 저장한다.
두 번째 지점의 경우에는 왼쪽 지점과 위쪽 지점이 모두 존재하므로 두 지점의 값 중 최소값과 현재 지점의 값을 더하여 현재 지점의 값으로 저장한다.

같은 방법으로 마지막 행까지 탐색을 마치면 가장 오른쪽 아래의 값이 경로의 최소값이 된다.

최종 코드
class Solution {
public int minPathSum(int[][] grid) {
// (0,0) 지점부터 오른쪽 방향으로 탐색
for(int i = 0; i < grid.length; i++) {
// 오른쪽 방향 탐색이 끝나면 아래쪽 방향 탐색
for(int j = 0; j < grid[0].length; j++) {
// (0,0) 지점은 탐색 제외
if(i == 0 && j == 0) continue;
// 가장 위쪽 지점 탐색중인 경우
if(i == 0) {
// 현재 지점의 값과 왼쪽 지점의 값의 합을 현재 지점에 저장
grid[i][j] += grid[i][j - 1];
}
// 가장 왼쪽 지점를 탐색중인 경우
else if(j == 0) {
// 현재 지점의 값과 위쪽 지점의 값의 합을 현재 지점에 저장
grid[i][j] += grid[i - 1][j];
}
// 그 외의 경우
else {
// 왼쪽 지점의 값과 위쪽 지점의 값 중 최소값을 현재 지점의 값과 더하여 저장
grid[i][j] += Math.min(grid[i][j - 1], grid[i - 1][j]);
}
}
}
// 도착점의 값을 return
return grid[grid.length - 1][grid[0].length - 1];
}
}
'알고리즘 > LeetCode' 카테고리의 다른 글
| [LeetCode] 1402. Reducing Dishes - Java/Dart (0) | 2023.03.29 |
|---|---|
| [LeetCode] 983. Minimum Cost For Tickets - Java/Dart (0) | 2023.03.28 |
| [LeetCode] 105. Construct Binary Tree from Preorder and Inorder Traversal - Java (0) | 2023.03.24 |
| [LeetCode] 1319. Number of Operations to Make Network Connected - Java (0) | 2023.03.24 |
| [LeetCode] 2348. Number of Zero-Filled Subarrays - Java (0) | 2023.03.21 |
