https://leetcode.com/problems/number-of-operations-to-make-network-connected/description/
Number of Operations to Make Network Connected - LeetCode
Can you solve this real interview question? Number of Operations to Make Network Connected - There are n computers numbered from 0 to n - 1 connected by ethernet cables connections forming a network where connections[i] = [ai, bi] represents a connection b
leetcode.com
문제
There are n computers numbered from 0 to n - 1 connected by ethernet cables connections forming a network where connections[i] = [ai, bi] represents a connection between computers ai and bi. Any computer can reach any other computer directly or indirectly through the network.
You are given an initial computer network connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.
Return the minimum number of times you need to do this in order to make all the computers connected. If it is not possible, return -1.
Example 1:
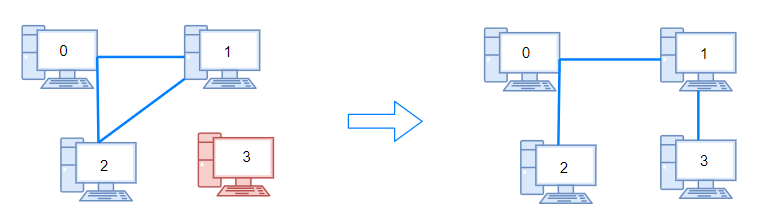
Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.
Example 2:

Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
Output: 2
Example 3:
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
Output: -1
Explanation: There are not enough cables.
Constraints:
- 1 <= n <= 105
- 1 <= connections.length <= min(n * (n - 1) / 2, 105)
- connections[i].length == 2
- 0 <= ai, bi < n
- ai != bi
- There are no repeated connections.
- No two computers are connected by more than one cable.
풀이
풀이 과정
0부터 n번까지의 컴퓨터가 있고 각 컴퓨터간의 연결 관계를 나타내는 2차원 배열 connections가 주어질 때 모든 컴퓨터가 연결 되기 위해서 케이블을 옮기는 과정의 최소 횟수를 구하는 문제이다. 만약 모든 컴퓨터를 연결하는 것이 불가능하다면 -1를 return한다.
이 문제에서 어떤 케이블을 어디에서 어디로 옮겨야 하는지는 크게 중요하지 않다.
n개의 노드를 모두 연결 시키기 위해서는 최소 n - 1개의 간선이 필요하다. 그렇기 때문에 만약 케이블의 개수를 나타내는 connections 배열의 길이가 n - 1보다 작은 경우에는 모든 컴퓨터를 연결하는 것이 불가능하다.
만약 케이블의 개수가 n - 1개 이상이라면 모든 컴퓨터를 연결하는 것이 가능하고 몇 번의 케이블 이동이 필요한지는 연결되어있지 않은 노드들의 개수만 파악하면 된다. 즉 비연결 그래프안에서 연결 그래프가 몇개나 있는지 탐색하는 것으로 생각하면 쉽게 풀이할 수 있다.
우선 탐색을 위해 사용할 변수를 선언해준다.
graph는 각 노드간의 연결관계를 저장할 리스트 변수이고 visited는 특정 노드에 방문을 했는지 여부를 저장하기 위한 배열이다.
List<ArrayList<Integer>> graph = new ArrayList<>();
boolean[] visited;
케이블의 개수가 n - 1개보다 적다면 연결이 불가능하므로 바로 -1을 return 해준다.
// n개의 컴퓨터를 모두 연결하기 위한 케이블의 최소 개수는 n - 1개
// 케이블의 개수가 n - 1개보다 적다면 연결이 불가하므로 -1을 return
if(connections.length < n - 1) return answer;
visited와 graph 변수를 각각 초기화 해준다.
// 각 노드의 방문 여부를 저장할 배열
visited = new boolean[n];
// 각 컴퓨터별 노드 생성
for(int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
// 각 케이블의 연결 관계를 저장
for(int[] connection : connections) {
graph.get(connection[0]).add(connection[1]);
graph.get(connection[1]).add(connection[0]);
}
각 노드를 순회하며 방문 여부를 탐색하고 현재 노드와 연결된 모든 노드를 방문하며 방문 여부를 업데이트 한다.
만약 현재 노드가 처음 방문한 노드인 경우에는 다른 노드와 연결되어있지 않았던 경우이므로 정답 카운트를 증가시켜준다. 단. 최초 탐색인 경우에는 항상 방문 여부가 false로 시작하므로 정답 카운트 변수는 -1부터 시작한다.
int answer = -1;
// 각 노드를 탐색
for(int i = 0; i < n; i++) {
// 처음 방문 한 노드인 경우 다른 노드와 연결되어 있지 않았던 경우이므로 정답 카운트 증가
// 단, 최초 탐색인 경우 항상 방문 여부가 false이므로 정답 카운트는 -1부터 시작
// 현재 노드는 방문 처리하고 현재 노드와 연결된 모든 노드 탐색
if(!visited[i]) {
answer++;
visited[i] = true;
dfs(i);
}
}
현재 노드와 연결되어있는 다른 노드들을 탐색하는데는 다음 함수를 사용한다.
public void dfs(int node) {
// 현재 노드와 연결되어 있는 이웃 노드 탐색
for(int neighbor : graph.get(node)) {
// 처음 방문하는 노드인 경우 방문여부를 true로 바꾸고 다음 노드 탐색
if(!visited[neighbor]) {
visited[neighbor] = true;
dfs(neighbor);
}
}
}
최종적으로 구해진 정답을 return 한다.
return answer;최종 코드
class Solution {
List<ArrayList<Integer>> graph = new ArrayList<>();
boolean[] visited;
public int makeConnected(int n, int[][] connections) {
int answer = -1;
// n개의 컴퓨터를 모두 연결하기 위한 케이블의 최소 개수는 n - 1개
// 케이블의 개수가 n - 1개보다 적다면 연결이 불가하므로 -1을 return
if(connections.length < n - 1) return answer;
// 각 노드의 방문 여부를 저장할 배열
visited = new boolean[n];
// 각 컴퓨터별 노드 생성
for(int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
// 각 케이블의 연결 관계를 저장
for(int[] connection : connections) {
graph.get(connection[0]).add(connection[1]);
graph.get(connection[1]).add(connection[0]);
}
// 각 노드를 탐색
for(int i = 0; i < n; i++) {
// 처음 방문 한 노드인 경우 다른 노드와 연결되어 있지 않았던 경우이므로 정답 카운트 증가
// 단, 최초 탐색인 경우 항상 방문 여부가 false이므로 정답 카운트는 -1부터 시작
// 현재 노드는 방문 처리하고 현재 노드와 연결된 모든 노드 탐색
if(!visited[i]) {
answer++;
visited[i] = true;
dfs(i);
}
}
return answer;
}
public void dfs(int node) {
// 현재 노드와 연결되어 있는 이웃 노드 탐색
for(int neighbor : graph.get(node)) {
// 처음 방문하는 노드인 경우 방문여부를 true로 바꾸고 다음 노드 탐색
if(!visited[neighbor]) {
visited[neighbor] = true;
dfs(neighbor);
}
}
}
}
'알고리즘 > LeetCode' 카테고리의 다른 글
| [LeetCode] 64. Minimum Path Sum - Java (0) | 2023.03.27 |
|---|---|
| [LeetCode] 105. Construct Binary Tree from Preorder and Inorder Traversal - Java (0) | 2023.03.24 |
| [LeetCode] 2348. Number of Zero-Filled Subarrays - Java (0) | 2023.03.21 |
| [LeetCode] 605. Can Place Flowers - Java (0) | 2023.03.20 |
| [LeetCode] 211. Design Add and Search Words Data Structure - Java (0) | 2023.02.26 |
