https://leetcode.com/problems/implement-trie-prefix-tree/
Implement Trie (Prefix Tree) - LeetCode
Can you solve this real interview question? Implement Trie (Prefix Tree) - A trie [https://en.wikipedia.org/wiki/Trie] (pronounced as "try") or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There
leetcode.com
문제
A trie (pronounced as "try") or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.
Implement the Trie class:
- Trie() Initializes the trie object.
- void insert(String word) Inserts the string word into the trie.
- boolean search(String word) Returns true if the string word is in the trie (i.e., was inserted before), and false otherwise.
- boolean startsWith(String prefix) Returns true if there is a previously inserted string word that has the prefix prefix, and false otherwise.
Example 1:
Input
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
Output
[null, null, true, false, true, null, true]
Explanation
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // return True
trie.search("app"); // return False
trie.startsWith("app"); // return True
trie.insert("app");
trie.search("app"); // return True
Constraints:
- 1 <= word.length, prefix.length <= 2000
- word and prefix consist only of lowercase English letters.
- At most 3 * 104 calls in total will be made to insert, search, and startsWith.
풀이
풀이 과정
Trie ( prefix tree ) 자료구조는 문자열 데이터를 효율적으로 저장하고 찾는데 사용하는 트리 데이터 구조의 한 종류이다. 때문에 자동완성이나 맞춤법 검사등의 프로그램에 사용된다.
주어진 조건에 따라서 Trie 구조를 이용한 문자열 검색기능을 만들어야하는 문제이다.
구현 해야하는 클래스는 새로운 Trie를 생성하기위한 클래스 Trie, 단어 저장을 위한 insert, 단어 탐색을 위한 search, 주어진 문자로 시작하는 단어 탐색을 위한 startsWith이다.
먼저 구현하고자 하는 Trie의 구조를 그림으로 표현해보면 아래와 같다.
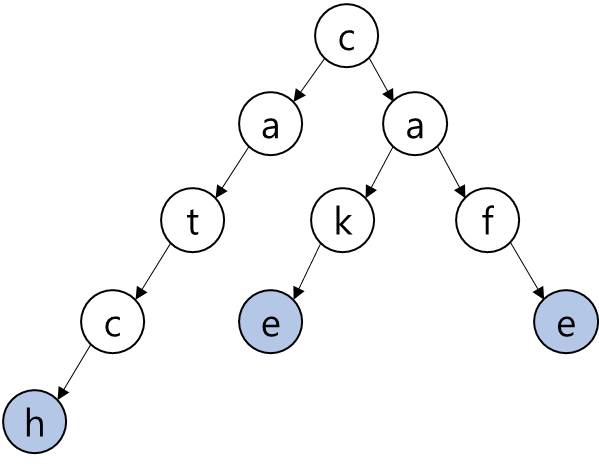
다음 구조는 "catch", "cake", "cafe" 3개의 단어를 저장하고 있는 Trie 트리이다.
파란색 바탕으로 칠해진 노드는 해당노드가 단어의 마지막 문자가 될 수 있다는 의미이다.
예를 들어 3개의 단어가 저장되어 있을 때 단어 "cat"을 찾고자 한다면 왼쪽 노드를 따라 "cat"이라는 단어가 연결되어 존재한다. 하지만 t가 단어의 끝이 아니기 때문에 "cat"이라는 단어는 현재 트리에 존재하지 않는다고 할 수 있다.
이러한 구조를 코드로 구현하기 위해 우선 트리의 노드가 될 클래스를 구현한다.
노드 클래스는 현재 노드가 단어의 끝인지 아닌지 판단할 변수와 현재 노드의 자식노드를 저장할 Map으로 구성한다.
// 트리 노드
class Node {
// 현재 노드까지가 단어인지 아닌지 판단할 변수
boolean isWord;
// 현재 노드의 자식노드를 저장할 Map
Map<Character, Node> children = new HashMap<>();
}
본격적으로 문제에서 주어진 조건을 구현하기 위해 만들어둔 트리 노드를 변수로 선언하고 Trie 클래스에서 새로운 노드를 생성하여 노드 변수에 저장한다.
class Trie {
// 노드 변수 선언
Node root;
public Trie() {
// 새로운 루트 노드 생성
root = new Node();
}
...
다음으로 단어를 저장하는 insert 함수를 작성한다.
insert 함수 안에서는 선언한 노드 변수를 새로운 변수에 담고 주어진 단어를 각 문자별로 반복하여 탐색한다.
만약 현재 탐색중인 문자가 현재 노드의 자식 노드에 존재하지 않는 경우 노드를 새로 생성하여 자식 노드에 추가한다.
그 후 현재 노드를 현재 탐색중인 문자에 해당하는 자식노드로 갱신한다.
반복하여 탐색하고 문자열을 끝까지 탐색한 경우에는 현재 노드에 단어인지 아닌지의 여부를 업데이트한다.
public void insert(String word) {
// 트리 최상위 노드
Node node = root;
// 문자열 끝까지 탐색
for(int i = 0; i < word.length(); i++){
// 현재 탐색중인 문자
Character c = word.charAt(i);
// 자식 노드에 현재 탐색중인 문자가 없는 경우
if(!node.children.containsKey(c)){
// 노드를 새로 생성하고 자식노드에 삽입
node.children.put(c, new Node());
}
// 노드를 갱신
node = node.children.get(c);
// 문자열을 끝까지 탐색한 경우 단어 여부 업데이트
if(i == word.length() - 1){
node.isWord = true;
}
}
}
주어진 단어를 탐색하는 search와 주어진 단어로 시작하는 문자를 탐색하는 startsWith를 구현하는 과정은 거의 똑같다고 할 수 있다.
마찬가지로 주어진 문자를 처음부터 끝까지 탐색하며 자식 노드에 해당 문자가 존재하면 노드를 갱신해가며 자식노드를 따라가면 된다. 만약 문자열을 끝까지 탐색하기전에 자식 노드에 현재 탐색하는 문자가 존재하지 않는다면 주어진 단어는 존재하지 않는 단어이므로 바로 false를 return해주면 된다.
public boolean search(String word) {
// 트리 최상위 노드
Node node = root;
// 문자열 끝까지 탐색
for(int i = 0; i < word.length(); i++){
// 현재 탐색중인 문자
Character c = word.charAt(i);
// 자식 노드에 현재 탐색중인 문자가 존재하는 경우
// 해당 자식노드로 노드 갱신
if(node.children.containsKey(c)) node = node.children.get(c);
// 자식 노드에 현재 탐색중인 문자가 존재하지 않는 경우 false를 return
else return false;
}
// 마지막까지 탐색 후 현재 노드까지 단어가 존재하면 true 존재하지않으면 false를 return
return node.isWord? true : false;
}
search 함수와 startsWith 함수의 유일한 차이점은 마지막 return 조건이다.
search 함수 같은 경우에는 현재 노드가 단어가 될 수 있는 마지막 노드인지 여부를 체크해야하지만 startsWith 함수 같은 경우에는 단어 앞에 해당 문자만 포함이 되어있으면 되기 때문에 마지막 노드가 단어의 마지막이여도 되고 마지막이 아니여도 상관없이 true를 return할 수 있다.
public boolean startsWith(String prefix) {
// 트리 최상위 노드
Node node = root;
// 문자열 끝까지 탐색
for(int i = 0; i < prefix.length(); i++){
// 현재 탐색중인 문자
Character c = prefix.charAt(i);
// 자식 노드에 현재 탐색중인 문자가 존재하는 경우
// 해당 자식노드로 노드 갱신
if(node.children.containsKey(c)) node = node.children.get(c);
// 자식 노드에 현재 탐색중인 문자가 존재하지 않는 경우 false를 return
else return false;
}
// prefix 마지막 까지 탐색을 했다면 해당 prefix로 시작하는 단어 존재
return true;
}최종 코드
// 트리 노드
class Node {
// 현재 노드까지가 단어인지 아닌지 판단할 변수
boolean isWord;
// 현재 노드의 자식노드를 저장할 Map
Map<Character, Node> children = new HashMap<>();
}
class Trie {
// 노드 변수 선언
Node root;
public Trie() {
// 새로운 루트 노드 생성
root = new Node();
}
public void insert(String word) {
// 트리 최상위 노드
Node node = root;
// 문자열 끝까지 탐색
for(int i = 0; i < word.length(); i++){
// 현재 탐색중인 문자
Character c = word.charAt(i);
// 자식 노드에 현재 탐색중인 문자가 없는 경우
if(!node.children.containsKey(c)){
// 노드를 새로 생성하고 자식노드에 삽입
node.children.put(c, new Node());
}
// 노드를 갱신
node = node.children.get(c);
// 문자열을 끝까지 탐색한 경우 단어 여부 업데이트
if(i == word.length() - 1){
node.isWord = true;
}
}
}
public boolean search(String word) {
// 트리 최상위 노드
Node node = root;
// 문자열 끝까지 탐색
for(int i = 0; i < word.length(); i++){
// 현재 탐색중인 문자
Character c = word.charAt(i);
// 자식 노드에 현재 탐색중인 문자가 존재하는 경우
// 해당 자식노드로 노드 갱신
if(node.children.containsKey(c)) node = node.children.get(c);
// 자식 노드에 현재 탐색중인 문자가 존재하지 않는 경우 false를 return
else return false;
}
// 마지막까지 탐색 후 현재 노드까지 단어가 존재하면 true 존재하지않으면 false를 return
return node.isWord? true : false;
}
public boolean startsWith(String prefix) {
// 트리 최상위 노드
Node node = root;
// 문자열 끝까지 탐색
for(int i = 0; i < prefix.length(); i++){
// 현재 탐색중인 문자
Character c = prefix.charAt(i);
// 자식 노드에 현재 탐색중인 문자가 존재하는 경우
// 해당 자식노드로 노드 갱신
if(node.children.containsKey(c)) node = node.children.get(c);
// 자식 노드에 현재 탐색중인 문자가 존재하지 않는 경우 false를 return
else return false;
}
// prefix 마지막 까지 탐색을 했다면 해당 prefix로 시작하는 단어 존재
return true;
}
}
/**
* Your Trie object will be instantiated and called as such:
* Trie obj = new Trie();
* obj.insert(word);
* boolean param_2 = obj.search(word);
* boolean param_3 = obj.startsWith(prefix);
*/
'알고리즘 > LeetCode' 카테고리의 다른 글
| [LeetCode] 605. Can Place Flowers - Java (0) | 2023.03.20 |
|---|---|
| [LeetCode] 211. Design Add and Search Words Data Structure - Java (0) | 2023.02.26 |
| [LeetCode] 76. Minimum Window Substring - Java (0) | 2023.02.14 |
| [LeetCode] 647. Palindromic Substrings - Java (0) | 2023.02.12 |
| [LeetCode] 5. Longest Palindromic Substring - Java (0) | 2023.02.10 |
